R 向量的统计学分析

本章只描述 R 中用来分析向量的统计工具， 关于向量的基础概念及常用工具，请参见我之前的文章:

• R基础
• R的向量

简单的内省

常常用向量来表示一组随机变量或者一组测试数据，然后使用统计工具来对它进行各种估计、测试等。 为了方便描述这些分析和统计工作，现在使用一个含有较多数据的样本， 例如直接用 rnorm() 来生成1000个服从正态分布的随机数，并绘制散点图：

> x <- rnorm(1000) # 得到一组正态分布的伪随机数据
> plot(x)          # 绘制这个数据的散点图

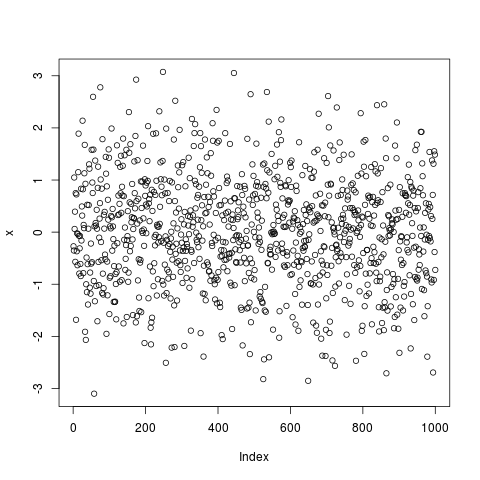服从正态分布的1000个伪随机样本

min()和max()分别求取向量的最小值和最大值。 而range()同时得到向量的最小值和最大值。

> min(x)
[1] -3.099832
> max(x)
[1] 3.074217
> range(x)
[1] -3.099832  3.074217

sum() 可以用来对一个向量求和。 sd() 可以得到向量的标准差。 var() 和 cov() 都可以用来计算一个向量的方差或者两个向量的协方差，cor() 可以用来计算 两个向量的相关系数(correlation)。

> sum(x)
[1] 4.60153
> sd(x)
[1] 1.040268
> var(x)
[1] 1.082157

协方差和相关系统发生在两个向量之间，所以还需要构造一个等长的向量来描述 cov() 和 cor() 的功能：

> y <- rnorm(1000)
> var(x,y)
[1] -0.005219245
> cov(x,y)
[1] -0.005219245
> cor(x,y)
[1] -0.004934983

从上面的结果知 var(x,y) 和 cov(x,y) 是一回事。x和y这两个随机样本的协方差很小， 说明这两个数据不太相似，并且相关系数也很小，就更能说明这两个数据是无关的了。 因为它们本来都是随机数据，两组随机数据自然应该是无关的了。

如果把这两组随机数据排一下序，由于它们都服从同样的分布，排序后应该会十分相似才 对。现在来验证一下。

> x.sort <- sort(x)
> y.sort <- sort(y)
> cov(x.sort, y.sort)
[1] 1.056269
> cor(x.sort, y.sort)
[1] 0.9987406

从上面的结果可以看出排序后的两个数据相似程度很高，相关系数接近了100%。

直观的数据分布情况

density() 得到一个向量的密度分布，用它可以把 x 的密度分布图形绘制出来。

> plot(density(x, bw="SJ"))    # 绘制密度分布曲线
> rug(jitter(x, amount=0.01))  # 在密度分布曲线下方绘制数据点

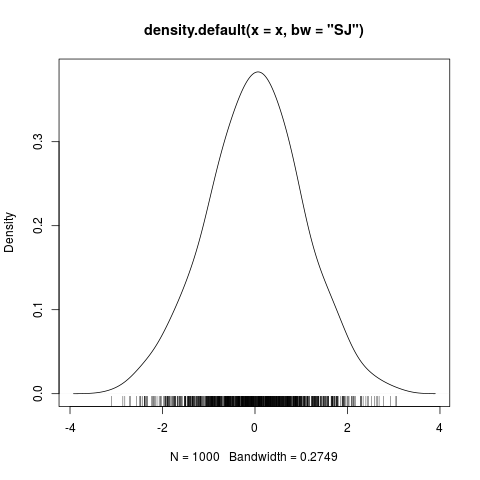x的密度分布

fivenum() 可以得到向量的5值表示，5值分别是最小值、低分位点、中位点、高分位点、最大值。

> fivenum(x)
[1] -3.09983208 -0.65490409  0.02000248  0.70135656  3.07421686

quantile() 可以获得向量的分位点。使用 quantile() 得到的分位点与 fivenum() 的 存在细微的区别， quantile() 使用的是估计值。

> quantile(x)
         0%         25%         50%         75%        100%
-3.09983208 -0.65330947  0.02000248  0.70109797  3.07421686

summary() 可以快速获得向量的整体印象，与quantile()类似，多一个平均值。 在拿到一份未知数据时，常常使用 summary() 来获得整体印象，并且常常配合 boxplot() 来了解异常数据等。

> summary(x)
     Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
-3.100000 -0.653300  0.020000  0.004602  0.701100  3.074000
> boxplot(x)

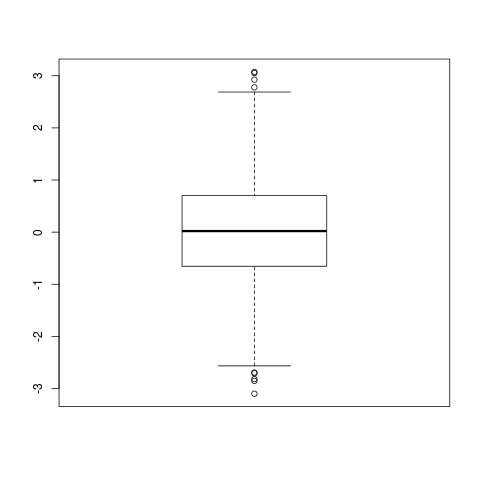x的整体印象

从boxplot()图中可以直观地了解到在上端和下端都存在几个数据点离整体分布比较远，有可能是异常数据。

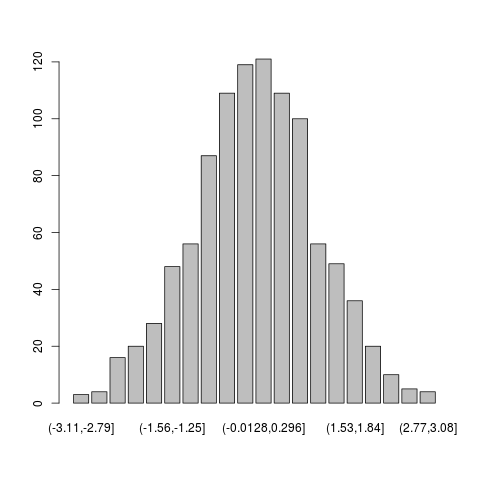
hist() 直接绘制出向量的统计直方图，它的效果与绘制 cut() 的效果相似：

> hist(x)
> plot(cut(x, 20))

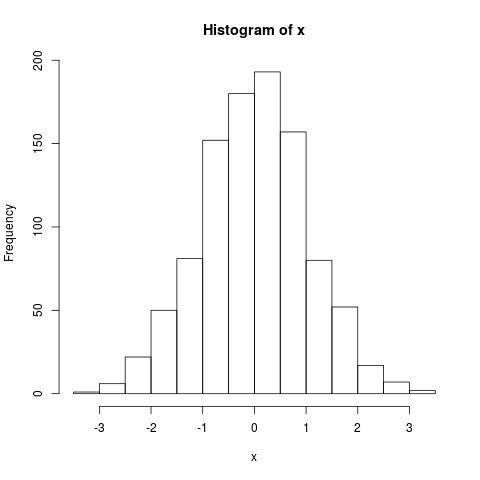x的统计直方图

x的cut图

数据分布的进阶分析

ecdf() 可以得到一个向量的经验积累分布函数。

> x.ecdf <- ecdf(x)
> plot(x.ecdf)

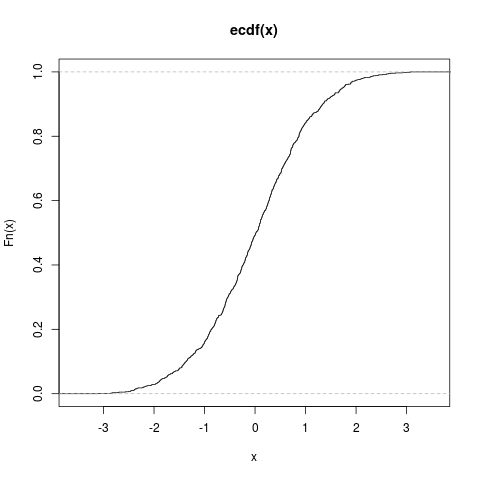x的经验积累分布函数曲线

需要注意的是 ecdf() 得到的是一个数值函数。

> x.x <- seq(min(x), max(x), len=21)
> plot(x.x, x.ecdf(x.x))

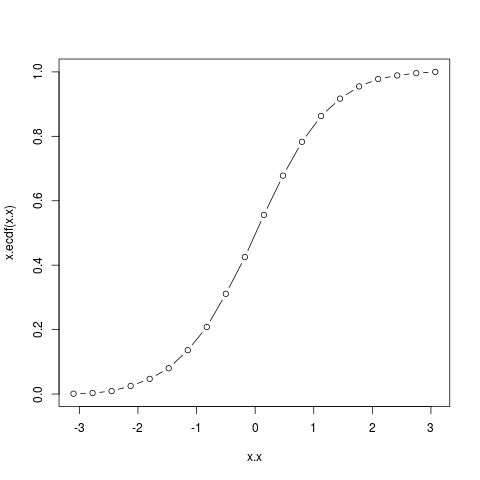经验积累分布曲线

cumsum() 积累求和函数。除了 ecdf() 之外，也可以使用 cumsum() 按如下的方法更加 精致的来绘制积累求和曲线，注意与 ecdf() 曲线的形状相同但纵轴的数值不同：

> x.r <- seq(min(x), max(x), len=20)     # 准备一个均匀的区间点
> x.c <- cut(x, x.r)                     # 按区间建立数据点的索引
> x.t <- table(x.c)                      # 统计每个区间上出现的数据点的个数，即统计直方图
> plot(x.r, cumsum(c(0,x.t)), type='b')  # 基于 cumsum() 绘制积累求和曲线

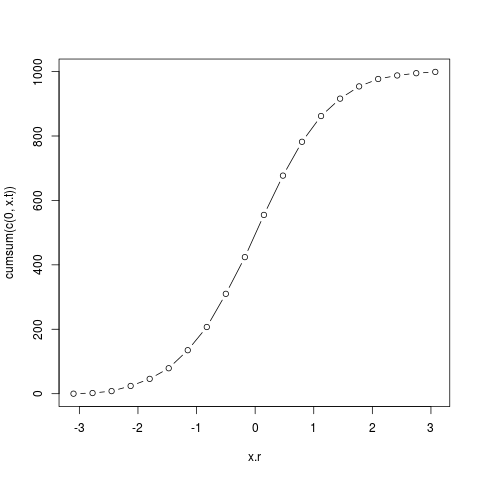cumsum 积累求和曲线

也可以画出排序后的数据点关于序号的图像，它的形状和 ecdf() 关于对角线对称，一般 用一个点来表示每个数据，这样就能看到数据的整体形态了，异常数据、离散情况等一目了然。

> plot(sort(x), pch='.')

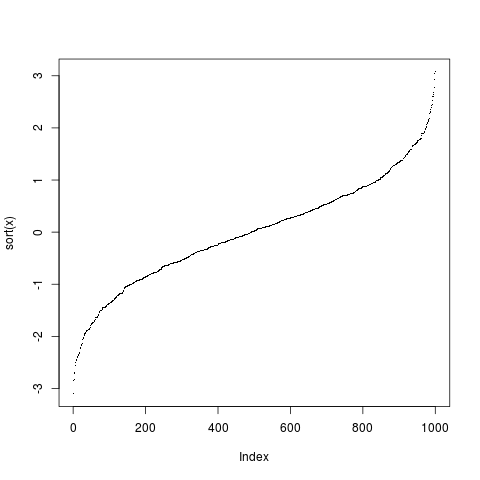数据排序散点图

pnorm() 正态分布的概率分布函数。可以用来对比一个数据的 ecdf() 曲线是否与正态 分布的概率分布函数相接近，由此来直观地判断这个数据是否服务正态分布。类似的，R中 还有大量概率分布模型的分布函数可以使用。

> plot(ecdf(x), do.points=FALSE, verticals=TRUE)         # 先画上数据的 ecdf 分布
> lines(x.r, pnorm(x.r, mean=mean(x), sd=sd(x)), col=2)  # 再叠加概率分布函数

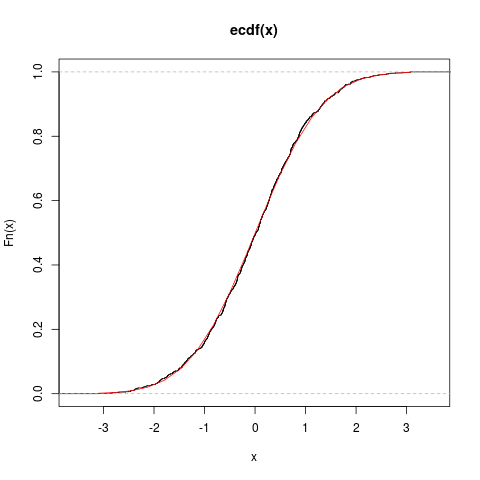概率分布曲线对比

qqnorm()和qqline() 对于正态分布，可以使用 qqnorm() 来绘制 q-q 图，即按正态 分布的分位点来标画数据的分位点，如果得到的点大致分布在 x=y 直线的附近，则直观地 说明数据服从正态分布。qqline() 则绘制当中的一条直线。

> qqnorm(x)
> qqline(x, lty=2, col=2)

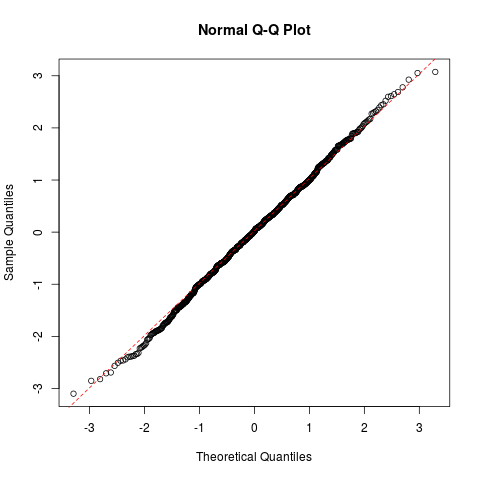正态分布Q-Q对比