对数据进行建模、拟合，我的经验是 当拿到一份数据时，先把它画出来，获得一些直观感受， 然后尝试从某个角度或者多个角度来理解这份数据， 按照对数据的理解整理成为数学模型， 最后就可以使用工具来解出这个模型。
R 的数值计算能力很强， 在 R 中可以十分方便地对数据进行建模、拟合。
比如我在做 aac-lc 音频解码程序时需要输入音频采样率数据， 通常情况下音频采样率数据是一个从几千Hz到几十万Hz之间的一个数。 但是在 aac-lc 音频编码中，常见的采样率只有几种（C语言表示）：
int r[] = {
96000, 88200, 64000, 48000, 44100, 32000,
24000, 22050, 16000, 12000, 11025, 8000
};
从而一个自然的想法就是把它定义为一个枚举，也就是把它们转换成另一串整数：
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
即用 0-11 中的每个数来表示原来的一个采样率，例如用 4 来表示 44100 (即 r[4] 的值为 44100)。 那么就多了一个任务，就是把原来采样率翻译成枚举值，也就是要从这组数中找 出与采样率相同的那个数，它的索引值就是这个枚举值，如果没有找到就报错。 对应的 C 代码简单如下:
#define NUM_OF_ELEMENT(array) (sizeof(array)/sizeof(array[0]))
int get_rate_index(int rate)
{
static int r[] = {
96000, 88200, 64000, 48000, 44100, 32000,
24000, 22050, 16000, 12000, 11025, 8000
};
int i;
for (i = 0; i < NUM_OF_ELEMENT(r); i++)
{
if (r[i] == rate)
{
return i;
}
}
return -1; // 没有找到对应的值
}
其实这里可以把索引值看成是关于采样率的函数，如果能找到函数解析式， 很有可能通过这个解析式计算出来比通过如上的方法查找出来要快。 想要找这个函数的解析式， R 可以帮上忙。先画上图来观察一下。
> r <- c( 96000, 88200, 64000, 48000, 44100, 32000,
+ 24000, 22050, 16000, 12000, 11025, 8000)
> idx <- 0:11
> plot(idx ~ r, type='b')
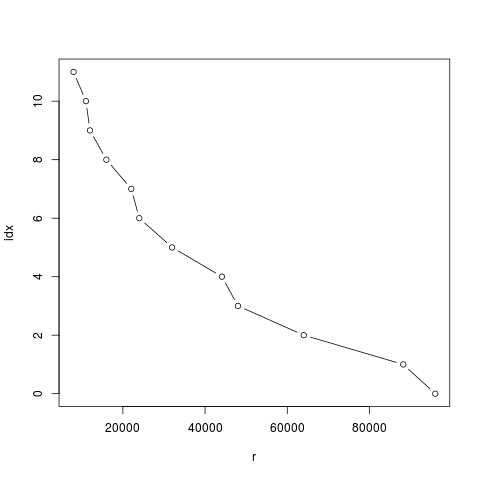* aac-lc采样率 *
在 R 中最简单的模型是线性模型，对于一个向量的线性模型就是一条直线。 可以使用 lm() 快速得到直线的拟合结果:
> f1 <- lm(idx ~ r)
> f1
Call:
lm(formula = idx ~ r)
Coefficients:
(Intercept) r
9.8995347 -0.0001134
注意到表达式 idx ~ r，表示的是 idx 按变量 r 变化的一个线性模型，相当于 $ idx = a r + b $。 上面的结果告诉我们，如果把这个函数理解成是直线，那么通过 lm() 求得的直线为
\( idx = 9.8995347 - 0.0001134 * r \)
在图上画出这条直线的效果如下图:
> plot(idx ~ r, type='b')
> abline(f1, lty=2, col=2)
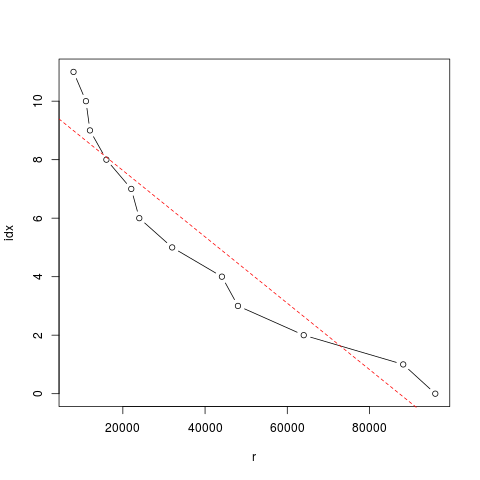aac-lc采样率的直线拟合
从这张图上来看，这条直线和原始的点拟合得不好。看来要换一个模型了。 通过观察，感觉可以把这个函数设计为如下形式:
\( f(x) = \frac{a}{x + b} + c \)
也就是函数中包含了一个分式、一个常数项。 在 R 中使用 nls() 来拟合一个非线性模型。
> f2 <- nls(idx ~ a/(r + b) + c, start=list(a=1,b=1,c=1))
Error in nlsModel(formula, mf, start, wts) :
singular gradient matrix at initial parameter estimates
当给定初始参数都为 1 的情况下，没有使模型快速收敛，R报出了错误信息。 这时需要对数据或模型进行改造，使得可以快速收敛。 改造的思路无外乎使数据的计算尽可能在-100到100之间， 初始参数选在一个实际存在的值上。
可以按第一个思路即把数据集变换到一个比较小的区间段，例如把 r 除以 10000 后再来拟合：
> x <- r / 10000
> f2 <- nls(idx ~ a/(x + b) + c, start=list(a=1,b=1,c=1))
> f2
Nonlinear regression model
model: idx ~ a/(x + b) + c
data: parent.frame()
a b c
54.214 2.874 -3.918
residual sum-of-squares: 1.004
Number of iterations to convergence: 8
Achieved convergence tolerance: 3.314e-06
这时拟合成功，残差为1.004，残差就是拟合值和实际值的差的平方和，这个值越小说明对结果拟合得越好。 在图上画出来:
> plot(idx ~ x, type='b')
> lines(x, predict(f2), lty=2, col=2)
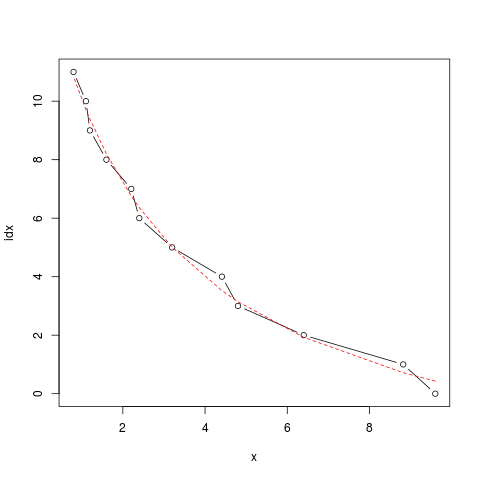aac-lc采样率的非线性拟合
从图上可以看出拟合得很好。因为索引值需要的是整数，试着计算一下:
> round(predict(f2))
[1] 0 1 2 3 4 5 6 7 8 9 10 11
发现在已知的值点上都对得上，所以就可以使用这个模型来直接计算了:
#define NUM_OF_ELEMENT(array) (sizeof(array)/sizeof(array[0]))
/*
* idx = a / (x + b) + c
* x = r / 10000
* a b c
* 54.214 2.874 -3.918
*/
int get_rate_index(int rate)
{
static int r[] = {
96000, 88200, 64000, 48000, 44100, 32000,
24000, 22050, 16000, 12000, 11025, 8000
};
double x = rate / 10000.0
int idx = round(54.214 / (x + 2.874) - 3.918);
if (r[idx] == rate)
return idx;
else
return -1; // 没有找到对应的值
}